Thống kê mô tả là gì?

Thống kê mô tả dùng cho mục đích thống kê trung bình cộng, tổng sum, độ lệch chuẩn,minimum,maximum, S.E mean, Kurtosis, Skewness, và cách sắp xếp kết quả theo Variable list, Alphabetic, tăng dần theo giá trị trung bình Ascending Means, giảm dần theo giá trị trung bình Descending Means…

Thông thường, thống kê mô tả người ta tập trung đánh giá vào giá trị nhỏ nhất, giá trị lớn nhất, giá trị trung bình. Còn giá trị độ lệch chuẩn ít được đánh giá, vì trong các bài nghiên cứu dạng khảo sát thị trường, giá trị này không thực sự quan trọng bằng các chỉ tiêu khác.

Cách chạy thống kê mô tả SPSS

Sau đây là minh họa thực hiện thống kê mô tả bằng hình ảnh, kèm theo file dữ liệu. Các bạn tải file dữ liệu ở đây nhé: phantichspss.com/filefordownload/thongkemota.sav

Đây là dữ liệu:

Chọn menu Analyze ->Descriptive statistics->Descriptive

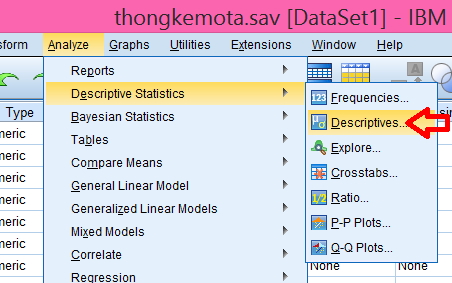
Sau đó các biến cần thống kê được đưa vào bên phải như trong hình

Sau đó nhấn nút OK nhé, kết quả thống kê mô tả sau hiện ra:

Giải thích ý nghĩa thống kê mô tả

Cột đầu tiên là tên các biến

Cột thứ 2 là N=200 , đây chính là số lượng người trả lời, số lượng mẫu.

Cột thứ 3 là minimum, là giá trị nhỏ nhất. Ví dụ giá trị nhỏ nhất của biến QUYETDINH3 là 2 thì nghĩa là trong 200 người trả lời này, sẽ có người trả lời ở mức 2. Và đây là mức thấp nhất( có nghĩa là không có người nào trả lời ở mức 1)

Cột thứ 4 là maximum, là giá trị lớn nhất. Ví dụ giá trị lớn nhất của biến QUYETDINH3 là 5 thì nghĩa là trong 200 người trả lời này, sẽ có người trả lời ở mức 5. Và đây là mức cao nhất.

Cột tiếp theo là mean, giá trị trung bình. Ví dụ mean của QUYETDINH1 là 3.45, thì mình có thể nó là đa số người ta đánh giá ở mức trên trung bình. ( vì mức trung bình là 3 trong thang đo likert 5). Giá trị này được tính bằng cách lấy trung bình cộng của 200 quan sát của biến QUYETDINH1. Nghĩa là lấy 200 giá trị này công lại, sau đó chia cho 200 thì sẽ ra được số này.

Cột cuối cùng là Std.Deviation độ lệch chuẩn. Độ lệch chuẩn là mức độ dao động của các biến xung quanh giá trị trung bình. Độ lệch chuẩn càng lớn thì quan điểm của người trả lời càng khác nhau. Ví dụ có hai trường hợp. Trường hợp 1: có ba số(-1,0,1) trường hợp 2 cũng có ba số: ( -100,0,100). Trong cả hai trường hợp thì giá trị trung bình của mỗi trường hợp đều bằng 0. Nhưng độ lệch chuẩn trong trường hợp thứ hai lớn hơn trong trường hợp thứ nhất nhiều nhé. Vì trường hợp đầu chỉ dao động nhỏ, giá trị lẩn quẩn ở mức 0 1… Còn trường hợp nhì dao động lớn, giá trị lên đến 100.